На главную

Лаборатория МЕХАНИКИ, НАВИГАЦИИ И УПРАВЛЕНИЯ ДВИЖЕНИЕМ

     Заведующий лабораторией – д.ф.-м.н., проф. Ю.Н. Челноков

     Состав лаборатории:
2 доктора и 3 кандидата наук; 1 научный сотрудник; 1 аспирант

Навигационное меню страницы

Основные направления и результаты научных исследований

Разработки прикладного характера

Основные публикации

Основные направления и результаты научных исследований

1. Кватернионные и бикватернионные модели и методы механики твердого тела, систем твердых тел и роботов-манипуляторов

2. Инерциальная ориентация, навигация и нелинейное инерциальное управление движением объектов на бесплатформенных принципах

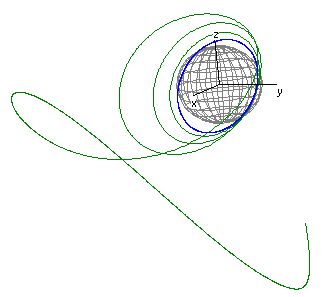
3. Оптимальное управление угловым и орбитальным движениями космических аппаратов с использованием кватернионных моделей астродинамики

4. Методы синтеза многосвязных систем автоматического управления по критериям точности и робастной устойчивости

5. Алгоритмическое обеспечение систем навигации и управления движением объектов различного назначения

     В рамках данных направлений:

• Разработаны новые кватернионные и бикватернионные модели и методы механики твердого тела и их систем, даны их приложения к исследованию движения твердого тела и гироскопических систем и установлению свойств их движения в нелинейной постановке

• Получено обобщение теоремы Гамильтона-Ишлинского о телесном угле на неголономное пространственное движение твердого тела, имеющее важные приложения в инерциальной навигации и управлении движением

• Предложен кватернионный метод регуляризации дифференциальных уравнений движения небесных и космических тел, имеющий ряд качественных преимуществ перед классическими регуляризациями Эйлера-Леви-Чивита и Кустаанхеймо-Штифеля; получены новые кватернионные регулярные дифференциальные уравнения возмущенной пространственной задачи двух тел и возмущенной пространственной ограниченной задачи трех тел

• Разработаны новые регулярные кватернионные модели механики космического полета, с их помощью решен ряд актуальных нелинейных пространственных задач оптимального управления траекторным движением космических аппаратов

• Предложена новая концепция теории устойчивости и управления движением твердого тела, основанная на фундаментальных теоремах теоретической механики – теоремах Эйлера-Даламбера и Шаля и новых дифференциальных уравнениях возмущенного движения

• Разработаны методы аналитического построения нелинейных управлений вращательным (угловым) движением твердого тела и космического аппарата (КА), гарантирующих асимптотическую устойчивость в большом или в целом любого выбранного программного углового движения и желаемую динамику управляемого углового движения твердого тела и космического аппарата, построены алгоритмы такого управления

• Построены новые кватернионные и бикватернионные уравнения и алгоритмы пространственной инерциальной навигации, в том числе регулярные кватернионные уравнения космической инерциальной навигации, а также новые уравнения и алгоритмы функционирования бесплатформенных инерциальных навигационных систем, реализованные в современных системах навигации на волоконно-оптических и лазерных гироскопах

• Предложен новый бикватернионный метод решения прямых задач кинематики роботов-манипуляторов, а также новый метод решения обратных задач кинематики роботов-манипуляторов, использующий бикватернионную теорию кинематического управления движением твердого тела

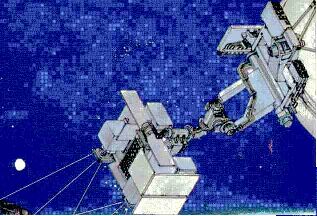
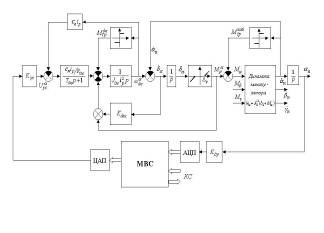
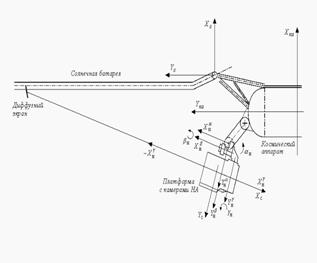
• Разработаны модели и алгоритмы управления движением уникального орбитального платформенного комплекса «Манипулятор – трехосная гиростабилизированная платформа» космического проекта «Марс-94»

• Предложены новые классы аналитических решений в задачах оптимальной переориентации твёрдого тела (КА) для различных функционалов качества переходных процессов

• Получены аналитические решения задач оптимальных разворотов КА снабжённых импульсными двигателями ориентации, реализующие двухимпульсные схемы управления; данные решения справедливы при произвольных граничных условиях по угловому положению и угловой скорости КА

• Исследованы особые режимы управления в задачах оптимальных разворотов сферически-симметричного, осесимметричного и произвольного твёрдого тела (КА) при произвольных граничных условиях задач

• Получено аналитическое решение модифицированной задачи оптимального разворота КА в классе обобщенных конических движений, которое может рассматриваться как приближенное решение классической задачи оптимального разворота КА при произвольных граничных условиях и произвольной динамической конфигурации КА

• Разработаны аналитические методы синтеза регуляторов многомерных систем управления с учетом требований точности при постоянных или случайных возмущениях и требований грубости (робастной устойчивости) замкнутой системы к возможным неопределенностям модели объекта

• Даны оценки предельной статической точности дискретных систем с регуляторами по состоянию и по измеряемому выходу

• Предложен новый класс дискретных регуляторов с наблюдателями минимального порядка и максимального быстродействия, основанный на приведении объекта управления к канонической форме

• Дано новое решение регулярных и сингулярных задач Н∞-оптимизации с использованием наблюдателей полного порядка и минимальной размерности, основанное на принципе разделения

     Фундаментальные НИР, выполненные в лаборатории по программам Отделения энергетики, машиностроения, механики и процессов управления РАН (1996-2015 гг.):

     “Кватернионное построение оптимальных управлений и траекторий космических аппаратов” (ГР № 01.960.0 04385, 1996-1997гг.),

     “Анализ и синтез законов управления движением в ньютоновском гравитационном поле на основе кватернионных методов механики и методов пространства состояний” (ГР № 01.9.80 0 02098, 1998 - 2000 гг.),

     “Разработка теории управления движением на основе кватернионных и бикватернионных методов механики твердого тела и методов пространства состояний и ее приложение к управлению движением космических аппаратов и роботов-манипуляторов” (ГР № 01.2.00 102218, 2001-2003 гг.),

     “Разработка кватернионных и бикватернионных моделей и методов механики твердого тела, методов пространства состояний в задачах динамики и управления движением” (ГР № 0120.0 403260, 2004-2006 гг.),

     “Кватернионные модели и методы динамики, навигации и управления движением” (ГР № 01.2.007 02554, 2007-2009 гг.),

     “Кватернионные модели и методы в задачах механики, навигации и управления движением” (ГР № 01201000279, 2010-
2012 гг.),

     “Исследование проблем механики, навигации и управления движением с использованием кватернионных и бикватернионных моделей и методов пространства состояний” (ГР № 01201352213, 2013-2015 гг.)

      Гранты, проекты:

      Проект в области авиационной и ракетно-космической техники:
     “Разработка теории и алгоритмов инерциальной навигации и управления движением летательных аппаратов на основе кватернионов Гамильтона и бикватернионов Клиффорда” (1993-1995 гг.).

     Проект по программе “Государственная поддержка интеграции высшего образования и фундаментальных наук на 1997-2000 гг.”:
    “Поддержка и развитие учебно-научного центра по проблемам механики Саратовского научно-образовательного комплекса в области фундаментальных наук”, раздел “Динамика, устойчивость и управление движением твердого тела”.

     Семь трёхгодичных проектов (1993-2014 гг.), поддержанных Российским фондом фундаментальных исследований:
    “Разработка кватернионных и бикватернионных моделей, методов и алгоритмов решения задач механики, навигации и управления движением” (1993-1995 гг., проект № 93-01-17479),
    “Кватернионные модели и методы теории управления движением космических аппаратов” (1996-1998 гг., проект № 96-01-01251),
    “Развитие кватернионных моделей и методов механики космического полета” (1999-2001 гг., проект № 99-01-00192),
    “Кватернионные модели и методы в пространственных нелинейных задачах оптимального управления движением космических аппаратов” (2002–2004 гг., проект № 02-01-00988),
    “Кватернионные модели и методы динамики и управления движением космических аппаратов” (2005–2007 гг., проект № 05-01-00-347),
    “Управление движением в космосе с использованием кватернионов” (2008–2010 гг., проект № 08-01-00-310),
    “Исследование проблем механики управляемого движения с использованием кватернионных и бикватернионных моделей и методов” (2012–2014 гг., проект № 12-01-00165).

     Двухгодичный проект в рамках научной программы “Университеты России – Фундаментальные исследования”:
   “Разработка аналитических и численных методов решения задач оптимального управления пространственным движением космических аппаратов, использующих кватернионные переменные”, выполненный  (2000-2001 гг.).

     Три издательских проекта, выполненных при поддержке Российского фонда фундаментальных исследований:
     Издание монографии “Кватернионные и бикватернионные модели и методы механики твердого тела и их приложения. Геометрия и кинематика движения” (2005–2006 гг., проект № 05-01-14038-д),
     Издание монографии “Кватернионные модели и методы динамики, навигации и управления движением” (2009-2010 гг., проект № 09-01-07022-д),
     Издание монографии “Кватернионные модели и методы динамики, навигации и управления движением” (2009 г., проект № 09-01-02002-э_д).

     Прикладные НИР, выполненные в рамках Государственного космического проекта “Марс-94” (1990-1996 гг.) по заказам Всероссийского НИИ транспортного машиностроения (г. С.-Петербург) и Института космических исследований РАН (г. Москва)

     Прикладные исследования по разработке теории, алгоритмов и программно-математического обеспечения функционирования бесплатформенных инерциальных навигационных систем, предназначенных для решения задач ориентации и навигации летательных и других аппаратов в географической и ортодромической системах координат по заказам Конструкторского бюро промышленной автоматики (г. Саратов, 1984-1990 гг.), ООО НПК “Оптолинк” (г. Москва (Зеленоград), 2006-2009 гг.), ОАО «Концерн «Авионика» (г. Москва, 2011 г.), ООО «Аэроспецпроект» (г. Жуковский Московской области, 2012-2013 гг.).

Назад к Навигационному меню

Разработки прикладного характера

Разработка математического, алгоритмического и программного обеспечения
бесплатформенной инерциальной навигационной системы (БИНС)

     Сотрудниками лаборатории разработано математическое, алгоритмическое и программное обеспечение БИНС, предназначенной для высокоточного решения задач инерциальной ориентации и навигации объекта в инерциальной или географической опорной системе координат в автономном и корректируемом режимах. Предполагается, что БИНС имеет в своем составе три акселерометра, измерители проекций абсолютной угловой скорости объекта, датчики высоты и вертикальной скорости (в корректируемом режиме) и бортовой вычислитель (БЦВМ).
     Разработаны новые высокоточные алгоритмы определения параметров ориентации объекта в инерциальной и географической системах координат (параметров Родрига-Гамильтона (Эйлера), углов курса, рыскания, тангажа и крена); проекций относительной, кажущейся и гравитационной скоростей, а также географических координат местоположения объекта (высоты, долготы и широты). Алгоритмы могут использовать или мгновенную первичную информацию о движении объекта (проекции векторов абсолютной угловой скорости и кажущегося ускорения объекта на связанные с ним координатные оси), или интегральную первичную информацию о движении объекта (приращения интегралов от проекций векторов абсолютной угловой скорости и кажущегося ускорения объекта). Для разработки алгоритмов использованы новые уравнения инерциальной ориентации и навигации, построенные сотрудниками лаборатории, а также применен новый эффективный математический аппарат, использующий кватернионы Гамильтона и бикватернионы Клиффорда.
     Разработанные алгоритмы ориентации БИНС имеют методические погрешности, равные 10^-8 ÷10^-5 град/час, а навигационные алгоритмы имеют в автономном режиме через час движения методические погрешности, равные 10^-5 ÷10^-3 м/с по скорости, и 10^-3 ÷4 м по местоположению (по вертикальному каналу эти погрешности на 1-2 порядка больше) в зависимости от параметров вращательного (углового) и траекторного (поступательного) движений объекта и порядка точности используемых алгоритмов.
     Рассмотрены основные принципы построения корректируемой по высоте и вертикальной скорости БИНС, предложены различные подходы к синтезу алгоритмов коррекции как для непрерывного, так и для дискретного вариантов. Разработан метод синтеза корректирующей обратной связи (в непрерывном и дискретном вариантах) с учетом помех в измерительной информации о высоте и вертикальной скорости с дополнительным требованием астатизма, необходимого для устранения постоянных составляющих ошибок вертикального канала. Проведено моделирование работы корректируемой БИНС с различными вариантами коррекции как без учета помех измерителей (гироскопов, акселерометров, датчиков высоты и вертикальной скорости), так и с учетом этих помех.
    Ряд разработок по БИНС выполнен по заказам Конструкторского бюро промышленной автоматики (г. Саратов, 1984-1990 гг.), ООО НПК “Оптолинк” (г. Москва (Зеленоград), 2006-2009 гг.), ОАО «Концерн «Авионика» (г. Москва, 2011 г.), ООО «Аэроспецпроект» (г. Жуковский Московской области, 2012-2013 гг.).

    Со списком публикаций сотрудников лаборатории по БИНС можно ознакомиться здесь.

Основные публикации

За период 1997-2015 гг. опубликовано свыше 130 научных работ, в том числе более 60 крупных научных статей в журналах «Известия РАН. Механика твердого тела», «Космические исследования», «Известия РАН. Теория и системы управления», «Гироскопия и навигация», «Автоматика и телемеханика».

Наверх

На главную